~Physics
/groups/physics/search/index.rss?tag=hotlist/groups/physics/search/?tag=hotWhat’s HotHotListHot!?tag=hot0/groups/physics/sidebar/HotListNo items tagged with hot.hot/groups/physics/search/index.rss?sort=modifiedDate&kind=all&sortDirection=reverse&excludePages=wiki/welcomelist/groups/physics/search/?sort=modifiedDate&kind=all&sortDirection=reverse&excludePages=wiki/welcomeRecent ChangesRecentChangesListUpdates?sort=modifiedDate&kind=all&sortDirection=reverse&excludePages=wiki/welcome0/groups/physics/sidebar/RecentChangesListmodifiedDateallRecent ChangesRecentChangesListUpdateswiki/welcomeNo recent changes.reverse5search
Motion----------------------------
Distance
distance = rate x time
This goes way back to your math classes using this formula. In our case, we use different names:
s = vt
where s is displacement (distance from your start) measured in meters, v is velocity (speed and direction) in meters/second and t is still time, usually measured in seconds.
We also use one version of this formula in calculating range: R = Vxt, where R is range in meters, Vx is velocity in the x direction, and t is time in seconds.
Acceleration:
When velocity changes (e.g. speeding up or slowing down) we describe this as acceleration. We use the letter a for this, and the units are meters/second squared or m/ss. Make sure you include these units whenever you answer a question.
You can see that if you multiply acceleration x time, the units would be velocity, so:
v = at
where v is velocity in m/s, a is acceleration in m/ss and t is time in seconds.
total displacement when something is acceleration can be found this way:
s = 1/2at^2
In a special case where something is falling, the a is the acceleration of gravity, or 9.8 m/ss.
There is another version of this formula that has no time:
Vf^2 = Vo^2 + 2as
where Vf^2 is final velocity, Vo^2 is the initial velocity, a is acceleration and s is displacement.
If the situation has no time measured or required, this is a handy relationship to use.
Energy----------------------
3 forms of energy were covered in our group:
PE is potential energy, the potential to fall to a lower height. The lowest height is called 0 PE
PE = mgh
where m is mass in kg, g is usually 9.8 (on earth) and h is height in meters
All forms of energy are measured in Joules, a handy measure of energy.
KE is energy of motion:
KE = 1/2 mv^2
where m is mass in kg, v is velocity in m/s and KE is measured in Joules (again). Note that there is no g in this equation, so it involves only mass and velocity.
SE is spring energy, or the energy stored in a spring.
Springs require force to be stretched. This force can be represented by this formula:
F = -kx
This means that if a spring is stretched, it will take a certain force (F) to stretch it a distance (x)
I know we used s for displacement and now we are using h for height and x for stretch, we are a whimsical science, what can I say?
Work or energy is Force • distance, so Energy = Force • distance would mean the energy stored in a spring would be these squared, but the spring has more force at the end, so we instead use this average:
SE = 1/2kx^2
where k is the stiffness of the spring in N/m (N is Newtons, a measure of force), and x is the amount the spring is stretched.
A good strategy in every problem is to ask yourself:
- is something able to fall?
- is something moving?
- is there a spring involved?
You can see that each of these refers to one of the formulas above.
Simple Harmonic Motion----------------
This is a mouthful, but it simply means that if one thing is moving back and forth, stopping at the ends, and moving quickly in the middle, we call it simple (one thing moving) harmonic (repeated) motion.
The ones you will likely see most of are the pendulum (pendula in plural) and the mass/spring system (like a person on a bungee cord)
Pendulum:
A pendulum needs three things: a mass (m), gravity (g) and some sort of cord (l)
If there is no gravity, there is no intention to fall to the bottom of the arc.
If there is no length, there is no way to raise above the equilibrium position at the bottom
If there is no mass, there is no force of gravity to move the system to a lower position
We describe period as the amount of time it takes to move from one end of the arc to the other and back again. We can also describe it as the time to move from one position to the same position moving IN THE SAME DIRECTION.
All SHM formulas are in the form T (period ) = 2π (something)^1/2:
Mass and spring:
In a mass/spring system, there is usually a mass, a spring and an equilibrium position. When the mass is pulled from this equilibrium position, and the spring exerts a force to restore it to this position, the amount of time it takes to get there and back to the same spot in the same direction is the period.
In short, this means if something is bouncing, the period is the amount of time it takes for the mass to return to the same place, moving in the same direction:
There are several other systems that "oscillate" in this fashion, you might see in the next few years.
Waves and Sound-----------------------
Waves can be described as transverse, meaning the wave displacement is 90° to the direction of travel (like sideways pulses on a spring), or longitudinal, meaning the displacement is along the direction of travel (like sound waves).
In both cases, the relationship between velocity, frequency and wavelength is:
V = f • wavelength
We use the character lambda for wavelength:
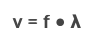
Velocity is measured in m/s, frequency is in cycles per second, and wavelength is in meters.
You may also see a formula about period, which is the inverse of frequency: T = 1/f
We also studied reflections, where pulses hit a hard boundary. When this happens, the wave reflects back in the opposite direction, on the opposite side of the pulse. We describe this as adding half of a wavelength.
So, to find the speed of sound, we can hold a tuning fork over an open tube, and when the sound wave travels down the tube (1/4 of a wavelength), bounces off the bottom (2/4 of a wavelength), and back (another 1/4 of a wavelength) it all adds up to 4/4 wavelength or one wave. This is a form of resonance.
Heat---------------------
We used two formulas for heat:
Q = mc∆t
Which describes the heat needed or released to change the temperature of a material.
In this formula, m is the mass of the material, c is the specific heat of the metal (the heat holding capacity) and ∆t is the temperature change of the material.
We heated pieces of metal and dropped them into water. The amount of heat released by the hot metal equaled the amount of heat gained by the water:
mc∆t = mc∆t
We used this to calculate the c value for the metal.
We then covered three modes of heat travel:
Conduction-heat travel by contact
Radiation-heat travel through emission (e.g. light)
Convection-heat travel by the movement of a material (e.g. hot water, air, steam)
To measure the movement of heat, we did an experiment involving the cooling of hot water to the room temperature.
Since this follows a law called Newton's law of cooling, we could compare the k (decay constant) of each system.
This is the same formula we use for radioactive decay, called the exponential decay formula:
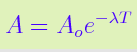
In each case, A is the amount left, or final temperature, Ao is the initial amount or initial temperature, e is the exponential decay formula, t is time in seconds, and the character next to it is called the decay constant. We use k for heat, and lambda for radioactive stuff.
We also used this formula to determine time of death in coroner cases. In these cases, the initial temperature was usually 37°C (body temperature). To use the formula, we find the difference between these temperatures and room temperature, for example in a room at 20°C, body temperature would be 17°C.
Radioactivity-----------------
One special case of this decay formula is when the amount left is 1/2 of the amount that started. We call the amount of time to do this the half-life.
One simple version of this formula is:
A = Ao (1/2)^n where n the number of half lives.
Note that this does not have to be a round number, e.g. if the half life is 8 days, 12 days would be n = 1.5
Comments